At the CodeMash conference this year many things stuck with me, and two have been bugging me enough to do something about them this last weekend. One was the idea that programmers need to practice and refine their skills, which was probably best described in the ideas of “Code Katas” ala Dave Thomas in the Pragmatic Programmer. The other was my recent concentration on all-things-Silverlight, specifically looking at the power of the platform and the emerging patters (e.g. MVVM).
So if I can find an hour or two to “practice my craft” without expecting this will ever result in production code – just for learning – what should I tackle? It hit me – “Fractals!!!”. It seems like every computer system and programming environment that I’ve gotten since the late 80s I have seen what I could do with some of the now-classic fractal algorithms. Inspiration for this also came from Corey Hanes great feature summary of another classic, the “Game of Life”.
This post isn’t intended to be a detailed primer on fractals, and specifically fractals resulting from an “iterated function system” or IFS, but here are the basics. Many systems in nature exhibit features that look very similar to each other. That is, leaves on a tree, mountains, crystal structures, cells, snowflakes, etc. How can we try to simulate these patterns in a simple system to generate complex results. The IFS routines in these systems are kind of like DNA in a cell. Each element in the current generation of a system doesn’t know where it came from, but does know how to create the next generation in the system. How about an example.
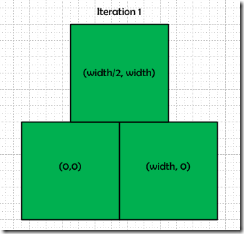
Start with a square.
The shape you start with really doesn’t matter. What you end up with is making a “collage” of whatever shape you start with, a square is simple and fills the space nicely (which will be important later).
Now we need to add some simple transformation rules. We’ll do a “classic” Serpinski triangle or “gasket”.
A transformation rule generally has four parts: Scale, Rotation, Translation, and Probability.
In this case each of the three translations will scale 50% on both axes and have no rotation (0 degrees).
- The first will not move at all (i.e. translate (0,0)).
- The second will be a full width horizontally away (width, 0).
- The third will be a full width vertically away and a half-width horizontally away (width/2, width)
These then are the simple rules that this system will run by. Each square in the system will know these rules and know how to apply them to themselves. So when told to “iterate” each square should execute each rule by creating a clone of itself, and applying the rule to it. After the iteration, the original square(s) should self-destruct as their short life is now over.
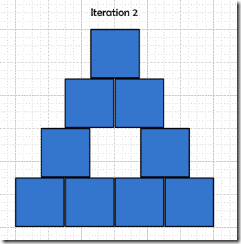
So what would happen with the next iteration?
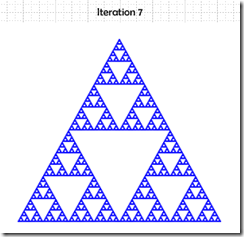
And so on and so on. What if we did this 7 times?
Starts looking far different that you might have expected.
So how might we start to tackle this in Silverlight?
Actually, this should be far easier to do in Silverlight than in previous platforms because graphics and transformations are built in to Silverlight “out-of-the-box”.
So “Iteration 0” will be easy (just a Rectangle).
<Rectangle Fill="Red" Height="400" Width="400"/>
Now we could create a rectangle with half the height, width, and translate it in XAML, but we want to be able to automate this, so perhaps there is a better way.
<Rectangle Fill="Blue" Height="400" Width="400"><Rectangle.RenderTransform><TransformGroup><ScaleTransform ScaleX=".5" ScaleY=".5"/><RotateTransform Angle="0"/><TranslateTransform X="0" Y="0"/></TransformGroup></Rectangle.RenderTransform></Rectangle>
We can take the original Rectangle and use the RenderTransform to handle all of the scaling, rotating, and translating of the Rectangle. This works pretty well and is starting to get promising. What would the other two “rules” look like?
<Rectangle Fill="LightBlue" Height="400" Width="400"><Rectangle.RenderTransform><TransformGroup><ScaleTransform ScaleX=".5" ScaleY=".5"/><RotateTransform Angle="0"/><TranslateTransform X="200" Y="0"/></TransformGroup></Rectangle.RenderTransform></Rectangle><Rectangle Fill="AliceBlue" Height="400" Width="400"><Rectangle.RenderTransform><TransformGroup><ScaleTransform ScaleX=".5" ScaleY=".5"/><RotateTransform Angle="0"/><TranslateTransform X="100" Y="200"/></TransformGroup></Rectangle.RenderTransform></Rectangle>
But now we have a problem. This works well for Iteration 1, but not for subsequent Iterations. We need to be able to do transformations on top of existing transformations (on top of other existing transformations, etc.). Rectangle alone will not get us there.
What is a very simple XAML object that can contain another object? The ContentControl is just such a basic object. Its basic job is to contain one other object (which itself could contain other objects), and it just so happens to also inherit from UIElement, which means it has RenderTransform as well. What does this mean.
It means that we can do something like this …
<ContentControl><ContentControl.RenderTransform><TransformGroup><ScaleTransform ScaleX=".5" ScaleY=".5"/><RotateTransform Angle="0"/><TranslateTransform X="0" Y="0"/></TransformGroup></ContentControl.RenderTransform><Rectangle Fill="Green" Height="400" Width="400"><Rectangle.RenderTransform><TransformGroup><ScaleTransform ScaleX=".5" ScaleY=".5"/><RotateTransform Angle="0"/><TranslateTransform X="0" Y="0"/></TransformGroup></Rectangle.RenderTransform></Rectangle></ContentControl>
… which, if you look at it, is the first rule in Iteration 2. That is, apply the first rule to an object that already had the first rule already applied to it. Now we’ll get a rectangle that is half the size of a half-sized rectangle (25%) and hasn’t rotated or moved from the origin at (0,0).
[End of Part 1]
Two more parts to this coming in the next few days:
- Part 1 – Fractals with TransformGroup and MessageBus
- Part 2 – Automating transformations by creating an IFS Content Control
- Part 3 – Wiring up the Iterations using a basic MessageBus implementation.
- Part 4 – But will it work for a fractal Fern?
- Part 5 – Lessons Learned (aka limitations of the MessageBus and recursion in Silverlight)
Ironically(?) It will end up taking 3-4 times as long to blog this as it actually took to code it, but there is learning in the blogging as well, so more coming soon.


Silverlight Kata: IFS Fractals: Automating the Transforms
The concepts seem complicated. I am a newbie, can you recommend a site for a newbie like me?